解析古典統計 (Frequentist)與貝氏統計 (Bayesian)之爭
古典統計 (Frequentist,又稱頻率統計)與貝氏統計 (Bayesian)之戰在學界延續了數十年,而一直以來,古典統計的理論與應用主宰著世界。我們在學校所學到的統計課程,以及實際在產業界的統計應用,大多都依循著古典統計的框架而走。在過去的年代,因為古典統計太過強勢,甚至讓許多使用貝氏的學者不敢承認自己信仰貝氏。鄉野傳說在1960年的美國總統大選時,統計學家John Tukey和他的團隊成功以貝氏統計的方法,搶先預測出John F. Kennedy能夠勝選成為總統,但Tukey本人抵死不認自己是貝氏學者,而他的團隊也絕口不提當年預測的細節。
假設我們今天想要知道某所大學內所有男學生的平均身高,姑且稱之為$\theta$。第一步我們假設男學生的身高服從常態分佈。再來,我們假設該常態分佈的族群變異數$\sigma^2$已知,所以我們僅需要關注平均數就好。
我雖然無法得知該所大學男學生平均身高的真實數值,但我能夠確定的是他是一個定值。我可以作的事情,是透過對男學生抽樣,算出樣本的平均數$\hat{\theta}$來估計該大學男學生的平均身高。我可以利用機率描述$\hat{\theta}$,但我無法利用機率來描述$\theta$,因為該參數並不是隨機值。
這樣的方式我們稱之為點估計,是古典統計的三大工具 (點估計、區間估計、假說檢定)之一。而一般最常用的點估計式叫作最大概似估計 (maximum likelihood estimator,MLE),在我先前的文章中,也有證明到樣本平均數即是常態分佈的平均數的MLE。
我同意該所大學男學生的平均身高是個未知數值,但我認為該未知數並非定值而是具有隨機性,因此我可以利用機率分布去配飾之。我會先設定男學生的平均身高服從一個「先驗分布」 (prior distribution),透過從族群抽樣後,我可以更新這個機率分布,稱之為「後驗分布」 (posterior distribution)。
以貝氏統計的角度來說,抽樣所得來的資料可以幫助我們縮小男學生平均身高的先驗分布,而使得後驗分布範圍更加精確。我們所知道的貝氏定理 (Bayes Theorem),也就是在這時候發揮作用:
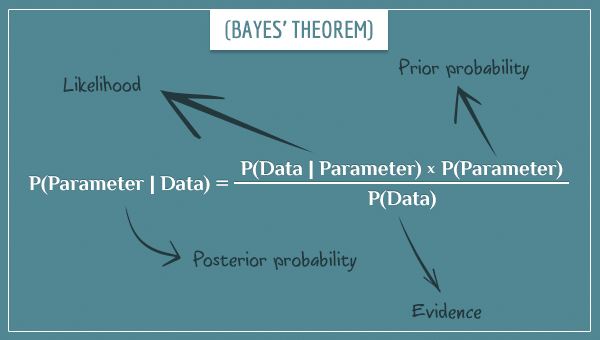
上圖貝氏定理中的Likelihood,即是我們熟悉的「抽樣分布」 (sampling distribution);而Evidence,則是在每個參數設定下,抽樣出該樣本的機率,所以Evidence我們一般也稱作Marginal likelihood。
如果我們好奇:該所大學男學生的平均身高介於170公分與180公分之間的機率,即$P(170 \leq \theta \leq 180)$。這樣的問題,以古典統計的角度來解析,無法回答。因為平均身高這個未知數值,在古典統計的框架之下,是一個定值,他要麼是介在170公分與180公分之間,要麼是在範圍之外,在這樣的情況下並不能用機率描述。古典統計能用機率描述的,是我們的估計式$\hat{\theta}$。聰明的你,可能覺得某個工具的形式和此題的數學式相當相似,在下一小節我們就會談到—信賴區間 (confidence interval)。
同樣的問題,相較之下對於貝氏統計來說,就沒有這層限制。因為從一開始,貝氏統計就是以機率分布的角度,去描述這個未知參數的行為。在貝氏的框架下,我進一步地將數學符號改寫成$P(170 \leq \Theta \leq 180)$,其中$\Theta$是為了強調平均身高這個未知參數,是一個隨機變數服從機率分布。
古典統計的推論基礎,建立在可持續重複抽樣的族群資料上 (repeated sample measurement)。信賴區間可以想像成是執行100次的抽樣,每一次的抽樣都依同樣的方式去算出上下界來建構區間。95%信心水準,代表是這100次內有95次抽樣所產生的區間,會包含我們估計的參數$\theta$。

透過圖的表示可以理解的更為清楚:欲估計的參數$\mu$以紅色虛線表示,是一個定值。每一次抽樣所產生的信賴區間,以藍色實線所表示。可以看到,有一些信賴區間,並沒有包含到參數$\mu$。包含到參數的比例,即是前述的信心水準 (confidence level)。
古典統計在大樣本的時候,透過中央極限定理 (Central Limit Theorem)的性質,在推論族群行為時非常的方便。相較於貝氏統計而言,古典統計並不仰賴先驗分布的設定。古典統計比較明顯的缺點,是缺乏較直觀的解釋,即便是存在已久被廣泛使用的信賴區間與假說檢定等,誤解這些工具意義的使用者仍不勝枚舉。
貝氏統計利用機率分布去描述任何未知參數,因此對於參數的隨機性有很好的解釋能力,這樣的性質讓貝氏統計在深度學習 (deep learning)的領域中逐漸受到重視。貝氏統計也適用於無法持續重複抽樣的資料分析 (例如特定候選人組合的總統大選),而且一般情況下並不需要利用大樣本的漸進特性 (asymptoticity)作推論。但貝氏也並非完全沒有缺點,即便目前科技的進展讓貝氏統計的後驗分布能夠被求出,但貝氏統計比起古典統計需要非常多的運算能力,仍是不爭的事實。
基礎的不同
那麼古典統計和貝氏統計究竟是差在哪裡呢?一般貝氏統計的根基—貝氏定理,都會在高等統計學或是機率論的課程中提到,但兩個系統的箇中差異,即便是統計系出生的學生,也不見得全部知道。其實,古典統計和貝氏統計在爭的,就是兩者對於「機率」 (probability)的運用上,有著最直接的不同:- 對古典統計來說,族群母數 (parameter,又稱參數)雖然未知,但是是一個定值。我們無法直接得知該母數的真實值,但可以透過對族群「抽樣」 (sampling),用以「估計」 (estimate)該母數與「推論」 (inference)該族群。對於古典統計而言,機率只會在抽樣的動作下才會有所意義。
- 對貝氏統計來說,任何未知的數值都可以用機率分布的概念去配飾之,而這個未知的數值,當然也可以包含未知的族群母數。相較之下,古典統計認為母數是一定值,自然也不會運用機率的概念去描述該母數。
還是有些霧煞煞?沒關係,直接用例子來作演繹:
假設我們今天想要知道某所大學內所有男學生的平均身高,姑且稱之為$\theta$。第一步我們假設男學生的身高服從常態分佈。再來,我們假設該常態分佈的族群變異數$\sigma^2$已知,所以我們僅需要關注平均數就好。
古典統計學家的回答
針對這樣的問題,古典統計學家會這樣回答:這樣的方式我們稱之為點估計,是古典統計的三大工具 (點估計、區間估計、假說檢定)之一。而一般最常用的點估計式叫作最大概似估計 (maximum likelihood estimator,MLE),在我先前的文章中,也有證明到樣本平均數即是常態分佈的平均數的MLE。
貝氏統計學家的回答
以貝氏統計的角度來說,抽樣所得來的資料可以幫助我們縮小男學生平均身高的先驗分布,而使得後驗分布範圍更加精確。我們所知道的貝氏定理 (Bayes Theorem),也就是在這時候發揮作用:

上圖貝氏定理中的Likelihood,即是我們熟悉的「抽樣分布」 (sampling distribution);而Evidence,則是在每個參數設定下,抽樣出該樣本的機率,所以Evidence我們一般也稱作Marginal likelihood。
如果我們好奇:該所大學男學生的平均身高介於170公分與180公分之間的機率,即$P(170 \leq \theta \leq 180)$。這樣的問題,以古典統計的角度來解析,無法回答。因為平均身高這個未知數值,在古典統計的框架之下,是一個定值,他要麼是介在170公分與180公分之間,要麼是在範圍之外,在這樣的情況下並不能用機率描述。古典統計能用機率描述的,是我們的估計式$\hat{\theta}$。聰明的你,可能覺得某個工具的形式和此題的數學式相當相似,在下一小節我們就會談到—信賴區間 (confidence interval)。
同樣的問題,相較之下對於貝氏統計來說,就沒有這層限制。因為從一開始,貝氏統計就是以機率分布的角度,去描述這個未知參數的行為。在貝氏的框架下,我進一步地將數學符號改寫成$P(170 \leq \Theta \leq 180)$,其中$\Theta$是為了強調平均身高這個未知參數,是一個隨機變數服從機率分布。
信賴區間
古典統計 - confidence interval
古典統計的信賴區間 (confidence interval),是統計學應用上非常被廣泛使用的工具之一。一般我們常見95%信賴區間,以數學符號表示為$P(u(X) \leq \theta \leq v(X))=0.95$,其中的下界$u(X)$和上界$v(X)$,是隨機變數$X$的函數。這95%信賴區間,最常被解讀成「參數$\theta$有95%的機會,會落在下界$u(X)$和上界$v(X)$之間」。很顯然地,透過前面的例子,我們知道這樣的解讀是錯的。因為古典統計框架下的參數是一個定值,並不會利用機率的形式去描述。那麼,信賴區間到底該怎麼解讀呢?古典統計的推論基礎,建立在可持續重複抽樣的族群資料上 (repeated sample measurement)。信賴區間可以想像成是執行100次的抽樣,每一次的抽樣都依同樣的方式去算出上下界來建構區間。95%信心水準,代表是這100次內有95次抽樣所產生的區間,會包含我們估計的參數$\theta$。

透過圖的表示可以理解的更為清楚:欲估計的參數$\mu$以紅色虛線表示,是一個定值。每一次抽樣所產生的信賴區間,以藍色實線所表示。可以看到,有一些信賴區間,並沒有包含到參數$\mu$。包含到參數的比例,即是前述的信心水準 (confidence level)。
貝氏統計 - credible interval
同樣有時都被翻作信賴區間,貝氏統計的credible interval和古典統計的confidence interval有著非常根本的不同。在閱讀相關文獻時,也得要注意相關名詞的誤解。在前述的例子我們已經提到過,貝氏框架下的母數會是一個機率分布,因此$P(u(x) \leq \Theta \leq v(x)|X=x)$,確實可以解讀成參數在某段區間內的機率。有注意到區間符號與confidence interval的不同嗎?這是因為confidence interval的隨機性,是來自於隨機變數$X$的估計式 (例如$\bar{X}$);而在給定的資料下 ($X=x$),credible interval的隨機性,則是來自於參數$\theta$本身。彼此的優劣
在現今的年代下,隨著電腦運算能力的提升,貝氏統計也逐漸受到人們的重視,並且在如人工智慧等領域有著廣泛應用。而古典統計,依然有著很顯著的影響力,例如企業廣泛運用的A/B test,基本上離不開古典統計的假說檢定。在彼此爭執的情況下,必然也會比較兩者各自的優點與劣勢。古典統計在大樣本的時候,透過中央極限定理 (Central Limit Theorem)的性質,在推論族群行為時非常的方便。相較於貝氏統計而言,古典統計並不仰賴先驗分布的設定。古典統計比較明顯的缺點,是缺乏較直觀的解釋,即便是存在已久被廣泛使用的信賴區間與假說檢定等,誤解這些工具意義的使用者仍不勝枚舉。
貝氏統計利用機率分布去描述任何未知參數,因此對於參數的隨機性有很好的解釋能力,這樣的性質讓貝氏統計在深度學習 (deep learning)的領域中逐漸受到重視。貝氏統計也適用於無法持續重複抽樣的資料分析 (例如特定候選人組合的總統大選),而且一般情況下並不需要利用大樣本的漸進特性 (asymptoticity)作推論。但貝氏也並非完全沒有缺點,即便目前科技的進展讓貝氏統計的後驗分布能夠被求出,但貝氏統計比起古典統計需要非常多的運算能力,仍是不爭的事實。

留言
張貼留言